10. Matplotlib

Contents

• Matplotlib

  • Overview

  • The APIs

  • More Features

  • Further Reading

  • Exercises

10.1. Overview

We’ve already generated quite a few figures in these lectures using Matplotlib.

Matplotlib is an outstanding graphics library, designed for scientific computing, with

• high-quality 2D and 3D plots

• output in all the usual formats (PDF, PNG, etc.)

• LaTeX integration

• fine-grained control over all aspects of presentation

• animation, etc.

10.1.1. Matplotlib’s Split Personality

Matplotlib is unusual in that it offers two different interfaces to plotting.

One is a simple MATLAB-style API (Application Programming Interface) that was written to help MATLAB refugees find a ready home.

The other is a more “Pythonic” object-oriented API.

For reasons described below, we recommend that you use the second API.

But first, let’s discuss the difference.

10.2. The APIs

10.2.1. The MATLAB-style API

Here’s the kind of easy example you might find in introductory treatments

%matplotlib inline
import matplotlib.pyplot as plt
plt.rcParams["figure.figsize"] = (10, 6) #set default figure size
import numpy as np

x = np.linspace(0, 10, 200)
y = np.sin(x)

plt.plot(x, y, 'b-', linewidth=2)
plt.show()

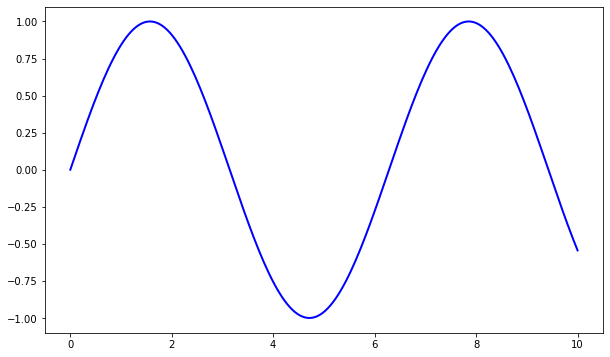
This is simple and convenient, but also somewhat limited and un-Pythonic.

For example, in the function calls, a lot of objects get created and passed around without making themselves known to the programmer.

Python programmers tend to prefer a more explicit style of programming (run import this in a code block and look at the second line).

This leads us to the alternative, object-oriented Matplotlib API.

10.2.2. The Object-Oriented API

Here’s the code corresponding to the preceding figure using the object-oriented API

fig, ax = plt.subplots()
ax.plot(x, y, 'b-', linewidth=2)
plt.show()

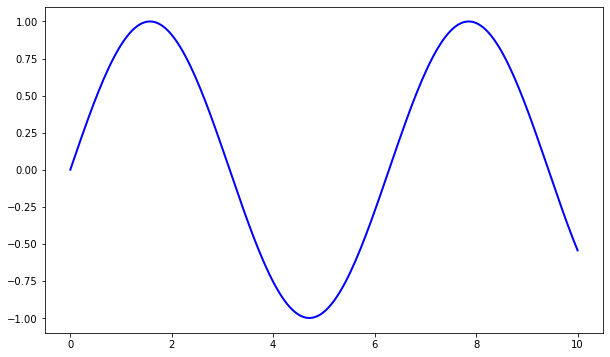
Here the call fig, ax = plt.subplots() returns a pair, where

• fig is a Figure instance—like a blank canvas.

• ax is an AxesSubplot instance—think of a frame for plotting in.

The plot() function is actually a method of ax.

While there’s a bit more typing, the more explicit use of objects gives us better control.

This will become more clear as we go along.

10.2.3. Tweaks

Here we’ve changed the line to red and added a legend

fig, ax = plt.subplots()
ax.plot(x, y, 'r-', linewidth=2, label='sine function', alpha=0.6)
ax.legend()
plt.show()

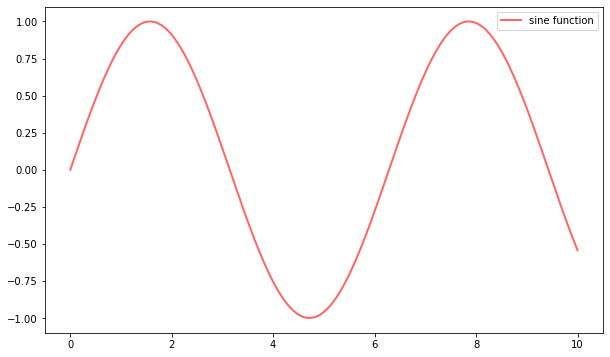
We’ve also used alpha to make the line slightly transparent—which makes it look smoother.

The location of the legend can be changed by replacing ax.legend() with ax.legend(loc='upper center').

fig, ax = plt.subplots()
ax.plot(x, y, 'r-', linewidth=2, label='sine function', alpha=0.6)
ax.legend(loc='upper center')
plt.show()

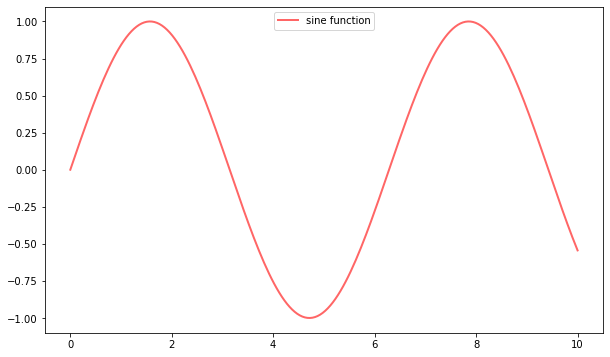
If everything is properly configured, then adding LaTeX is trivial

fig, ax = plt.subplots()
ax.plot(x, y, 'r-', linewidth=2, label='$y=\sin(x)$', alpha=0.6)
ax.legend(loc='upper center')
plt.show()

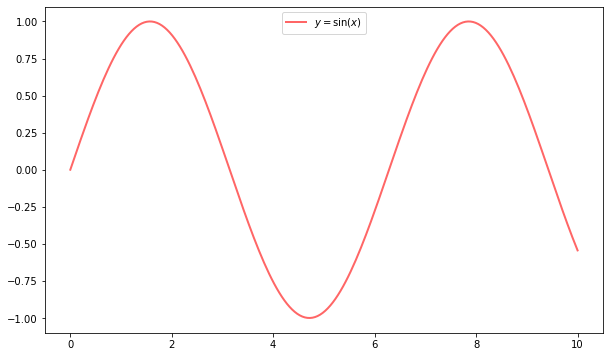
Controlling the ticks, adding titles and so on is also straightforward

fig, ax = plt.subplots()
ax.plot(x, y, 'r-', linewidth=2, label='$y=\sin(x)$', alpha=0.6)
ax.legend(loc='upper center')
ax.set_yticks([-1, 0, 1])
ax.set_title('Test plot')
plt.show()

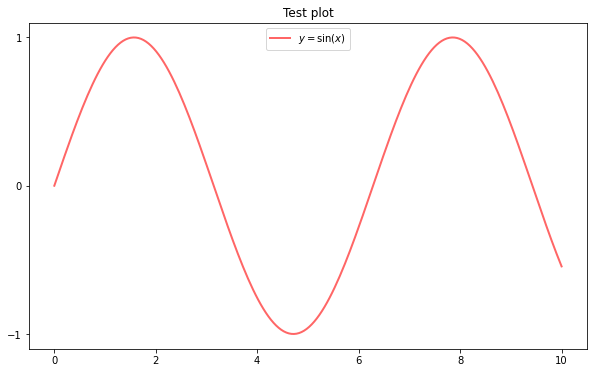
10.3. More Features

Matplotlib has a huge array of functions and features, which you can discover over time as you have need for them.

We mention just a few.

10.3.1. Multiple Plots on One Axis

It’s straightforward to generate multiple plots on the same axes.

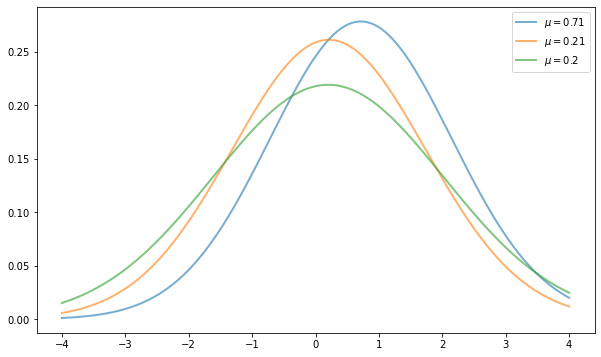
Here’s an example that randomly generates three normal densities and adds a label with their mean

from scipy.stats import norm
from random import uniform

fig, ax = plt.subplots()
x = np.linspace(-4, 4, 150)
for i in range(3):
    m, s = uniform(-1, 1), uniform(1, 2)
    y = norm.pdf(x, loc=m, scale=s)
    current_label = f'$\mu = {m:.2}$'
    ax.plot(x, y, linewidth=2, alpha=0.6, label=current_label)
ax.legend()
plt.show()

10.3.2. Multiple Subplots

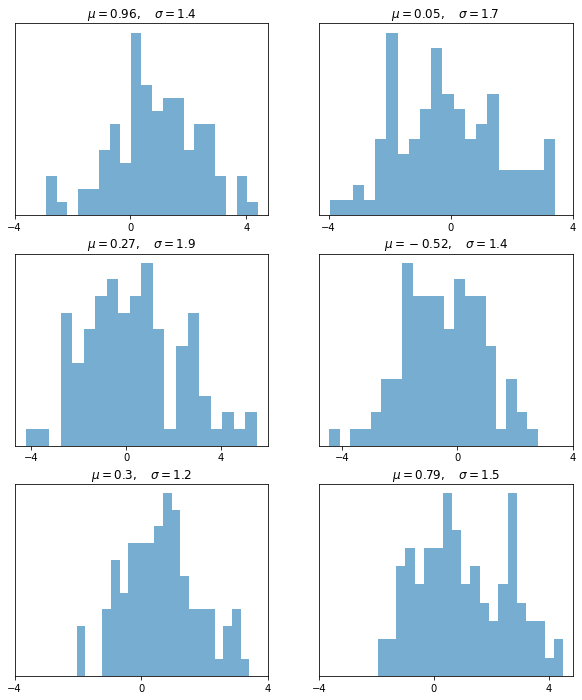
Sometimes we want multiple subplots in one figure.

Here’s an example that generates 6 histograms

num_rows, num_cols = 3, 2
fig, axes = plt.subplots(num_rows, num_cols, figsize=(10, 12))
for i in range(num_rows):
    for j in range(num_cols):
        m, s = uniform(-1, 1), uniform(1, 2)
        x = norm.rvs(loc=m, scale=s, size=100)
        axes[i, j].hist(x, alpha=0.6, bins=20)
        t = f'$\mu = {m:.2}, \quad \sigma = {s:.2}$'
        axes[i, j].set(title=t, xticks=[-4, 0, 4], yticks=[])
plt.show()

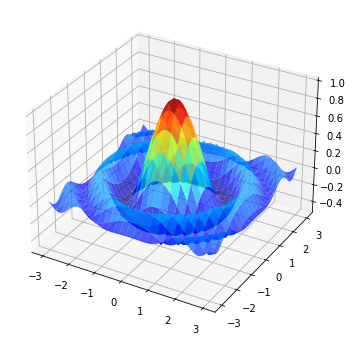
10.3.3. 3D Plots

Matplotlib does a nice job of 3D plots — here is one example

from mpl_toolkits.mplot3d.axes3d import Axes3D
from matplotlib import cm


def f(x, y):
    return np.cos(x**2 + y**2) / (1 + x**2 + y**2)

xgrid = np.linspace(-3, 3, 50)
ygrid = xgrid
x, y = np.meshgrid(xgrid, ygrid)

fig = plt.figure(figsize=(10, 6))
ax = fig.add_subplot(111, projection='3d')
ax.plot_surface(x,
                y,
                f(x, y),
                rstride=2, cstride=2,
                cmap=cm.jet,
                alpha=0.7,
                linewidth=0.25)
ax.set_zlim(-0.5, 1.0)
plt.show()

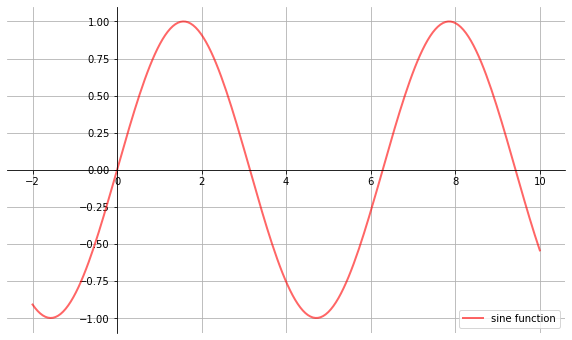
10.3.4. A Customizing Function

Perhaps you will find a set of customizations that you regularly use.

Suppose we usually prefer our axes to go through the origin, and to have a grid.

Here’s a nice example from Matthew Doty of how the object-oriented API can be used to build a custom subplots function that implements these changes.

Read carefully through the code and see if you can follow what’s going on

def subplots():
    "Custom subplots with axes through the origin"
    fig, ax = plt.subplots()

    # Set the axes through the origin
    for spine in ['left', 'bottom']:
        ax.spines[spine].set_position('zero')
    for spine in ['right', 'top']:
        ax.spines[spine].set_color('none')

    ax.grid()
    return fig, ax


fig, ax = subplots()  # Call the local version, not plt.subplots()
x = np.linspace(-2, 10, 200)
y = np.sin(x)
ax.plot(x, y, 'r-', linewidth=2, label='sine function', alpha=0.6)
ax.legend(loc='lower right')
plt.show()

The custom subplots function

1. calls the standard plt.subplots function internally to generate the fig, ax pair,

2. makes the desired customizations to ax, and

3. passes the fig, ax pair back to the calling code.

10.3.5. Style Sheets

Another useful feature in Matplotlib is style sheet.

We can use style sheets to create plots with uniform styles.

We can find a list of available style sheets by printing the attribute plt.style.available.

print(plt.style.available)

['Solarize_Light2', '_classic_test_patch', '_mpl-gallery', '_mpl-gallery-nogrid', 'bmh', 'classic', 'dark_background', 'fast', 'fivethirtyeight', 'ggplot', 'grayscale', 'seaborn', 'seaborn-bright', 'seaborn-colorblind', 'seaborn-dark', 'seaborn-dark-palette', 'seaborn-darkgrid', 'seaborn-deep', 'seaborn-muted', 'seaborn-notebook', 'seaborn-paper', 'seaborn-pastel', 'seaborn-poster', 'seaborn-talk', 'seaborn-ticks', 'seaborn-white', 'seaborn-whitegrid', 'tableau-colorblind10']

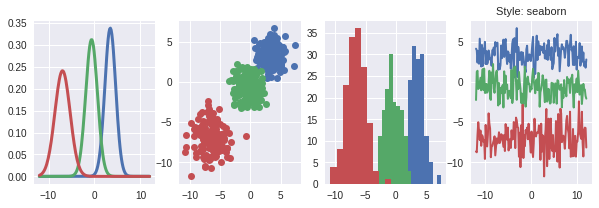
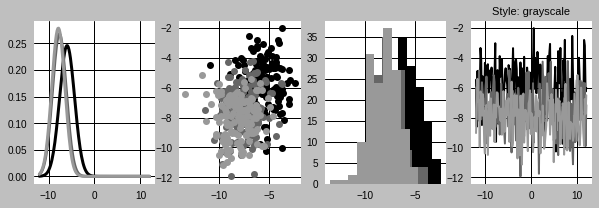
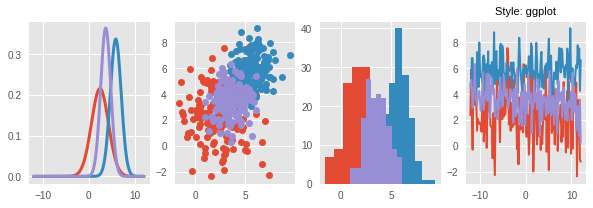
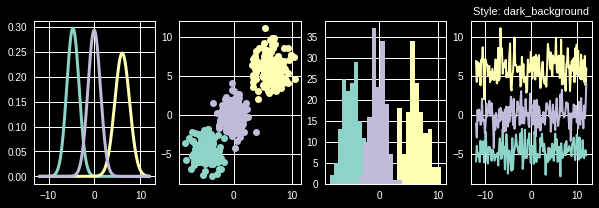
Let’s apply some of them to different types of visualizations

# Use four different style sheets
styles = ['seaborn', 'grayscale', 'ggplot', 'dark_background']

for i in range(4):

    # Set style sheet
    plt.style.use(styles[i])

    fig, axes = plt.subplots(nrows=1, ncols=4, figsize=(10, 3))
    x = np.linspace(-12, 12, 150)
    current_label = f'$\mu = {m:.2}$'

    for j in range(3):
        m, s = uniform(-10, 10), uniform(1, 2)
        y = norm.pdf(x, loc=m, scale=s)
        rnormX = norm.rvs(loc=m, scale=s, size=150)
        rnormY = norm.rvs(loc=m, scale=s, size=150)
        axes[0].plot(x, y, linewidth=3)
        axes[1].plot(rnormX, rnormY, ls='none', marker='o')
        axes[2].hist(rnormX)
        axes[3].plot(x, rnormY, linewidth=2)

    plt.title(f'Style: {styles[i]}', fontsize=11)

plt.show()

10.4. Further Reading

• The Matplotlib gallery provides many examples.

• A nice Matplotlib tutorial by Nicolas Rougier, Mike Muller and Gael Varoquaux.

• mpltools allows easy switching between plot styles.

• Seaborn facilitates common statistics plots in Matplotlib.

10.5. Exercises

Exercise 10.1

Plot the function

\[ f(x) = \cos(\pi \theta x) \exp(-x) \]

over the interval \([0, 5]\) for each \(\theta\) in np.linspace(0, 2, 10).

Place all the curves in the same figure.

The output should look like this

Solution to Exercise 10.1

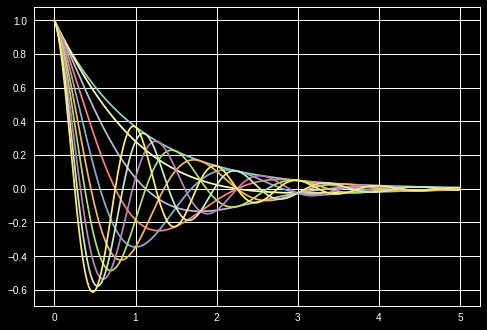
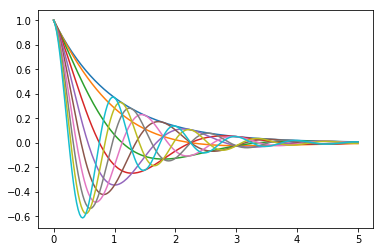
Here’s one solution

def f(x, θ):
    return np.cos(np.pi * θ * x ) * np.exp(- x)

θ_vals = np.linspace(0, 2, 10)
x = np.linspace(0, 5, 200)
fig, ax = plt.subplots()

for θ in θ_vals:
    ax.plot(x, f(x, θ))

plt.show()